Algorithm

数据结构

数组

栈结构

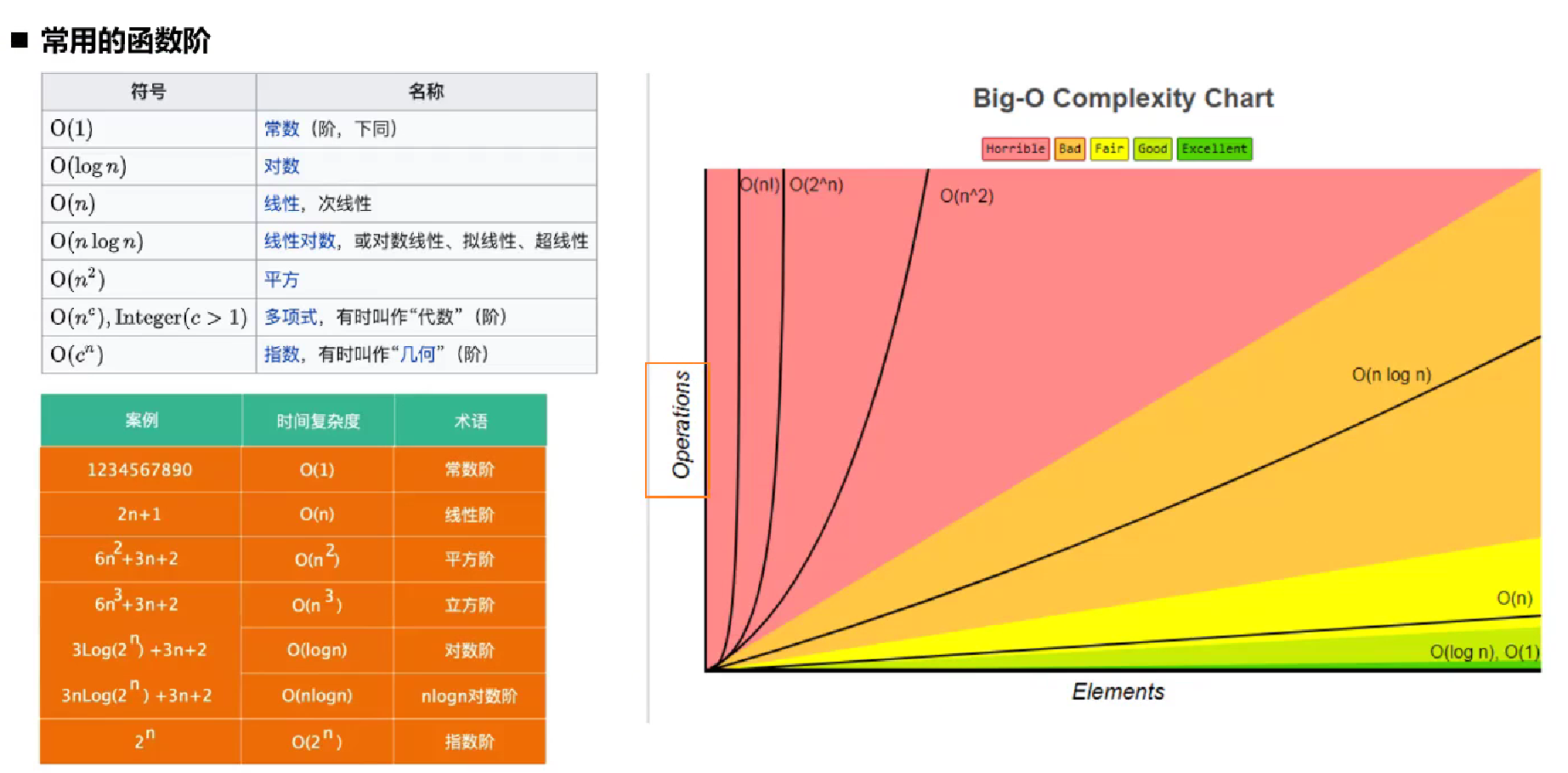
基础

  1. 先进后出
  2. 受限的线性结构

栈结构实现

  1. 基于数组

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    import IStack from "./type";

    //  封装一个栈
    class ArrayStack<T = any> implements IStack<T> {
        //  创建一个数组用来存储数组，外界访问不了
        private data: T[] = [];

        //  实现栈中的方法
        push(element: T): void {
            this.data.push(element);
        }
        pop(): T | undefined {
            return this.data.pop()
        }

        peek(): T | undefined {
            return this.data[this.data.length - 1]
        }

        isEmpty(): boolean {
            return this.data.length === 0
        }

        size(): number {
            return this.data.length
        }

    }

    //创建栈的实例 使用泛型
    // const stack = new ArrayStack<string>()
    //  确认是一个模块，不然会报错
    export default  ArrayStack

  2. 基于链表

十进制转二进制

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
//  把十进制的数据不断÷二，将求余的数用栈存起来，再依次弹栈
import ArrayStack from "./stack";
import Stack from "./stack";
function decimalToBinary(decimal: number): string {
    //  用于存放余数
    const stack = new ArrayStack<number>()
    //  不知道循环次数，使用while
    while (decimal > 0) {
        const result = decimal % 2
        stack.push(result)
        decimal = Math.floor(decimal / 2)
    }

    // 将数据全部弹栈 ,inEmpty有问题
    while (!stack.isEmpty()) {
        console.log(stack.pop())
    }
    // while (stack.size() != 0) {
    //     console.log(stack.pop())
    // }
    return ''
}
decimalToBinary(35)
export {}

有效的括号

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import ArrayStack from "./stack";

function isValid(s: string): boolean {
    // 遍历，遇到左括号将对应右括号存于栈中，遇到右括号，看看栈顶元素与之是否相同
    const stack = new ArrayStack()
    for(let i = 0; i<s.length; i++){
        const c = s[i]
        if (c === '(') {
            stack.push(')')
        }else if (c === '[') {
            stack.push(']')
        }else if (c === '{') {
            stack.push('}')
        } else {
           if( c !== stack.pop() ) return false

        }
    }
    return stack.isEmpty()
}

console.log(isValid("()"))
console.log(isValid("()[]{}"))
console.log(isValid("(]"))

队列

基础

  1. 先进先出
  2. 受限的线性结构

实现

  1. 基于数组

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    class ArrayQueue<T> {
        //  创建一个数组
        private data: T[] = []

        //  实现队列中的方法,队尾插入元素
        enqueue(element: T): void {
            this.data.push(element)
        }
        dequeue(): T | undefined {
            return this.data.shift()
        }

        peek(): T | undefined {
            return this.data[0]
        }

        isEmpty(): boolean {
            return this.data.length === 0
        }

        size(): number {
            return this.data.length
        }
        //	可以把他当成属性进行调用
        get size(): number {
            return this.data.length
        }
    }

    const queue = new ArrayQueue<string>()

  2. 基于链表

击鼓传花

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
//  循环，queue.size() === 1 结束
//  如果，数的数是1、2则出队再入队
//  如果是3则出队
//  返回 queue.dequeue();

import ArrayQueue from "./queue";

function hotPotato(names: any[], num: number) {
    const queue = new ArrayQueue<string>()
    //  将所有数据加入队列中
    for(const name of names) {
        queue.enqueue(name)
    }
    while (queue.size() > 1) {
       //  在循环中不需要淘汰
       for(let i = 0; i < num; i++) {
           const name = queue.dequeue()
           if (name) {
               queue.enqueue(name)
           }
       }
       // 不在循环中淘汰掉
       queue.dequeue()
   }
    return queue.dequeue()
}

const lastName = hotPotato(["John", "Tom", "Mary","Bob", "abs", "nsd", "qswd"], 4)
console.log(lastName)

约瑟夫环

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
//  约瑟夫环 一共多少人，每次淘汰第几个
import ArrayQueue from "./queue";

function lastRemaining(n: number, m: number) {
//    生成队列，将数据加入队列中
    const queue = new ArrayQueue<number>()
    for(let i = 0; i < n; i++) queue.enqueue(i)

    while (queue.size() > 1) {
    //    这里面遍历的数据需要重新加入队列中
        for (let i = 1; i < m; i++) {
            queue.enqueue(queue.dequeue()!)
        }
    //    淘汰掉
        queue.dequeue()
    }

    return queue.dequeue()!
}

console.log(lastRemaining(10,17))
const result = lastRemaining(5,3)
console.log(result)

链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
/**
 * 自己封装一个链表结构
 * 1. 封装两个类，一个类是节点，另一个类是链表
 * 2.节点 需要有值还有指向下一个节点
 * 3.链表 在里面实现方法，用户直接调用即可
 * */

class Node<T> {
    value: T
    next: Node<T> | null = null;
    constructor(value: T) {
        this.value = value
    }
}

class LinkList<T> {
    head: Node<T> | null = null;
    private size: number = 0;
    get length() {
        return this.size
    }

//    根据position传入的值，返回当前节点
    private getNode(position: number): Node<T> | null {
        //    获取对应节点值
        let current = this.head
        let index = 0
        while (index++ < position && current) {
            current = current.next
        }
        return  current
    }

//    在链表尾部追加数据
    append(value: T) {
    //    先创建一个节点
        const newNode = new Node(value);
    //    先判断头节点是否为空
        if(!this.head) {
            this.head = newNode
        }else {
        //    找到最后一只值
            let current = this.head
            while (current.next) {
                current = current.next
            }
            //  current指向最后一个节点
            current.next = newNode
        }
        this.size++
    }

//    遍历链表
    traverse() {
        const values: T[] = []
        let current = this.head
        while (current) {
            values.push(current.value)
            current = current.next
        }
        console.log(values.join("->"))
    }

//    插入方法
    insert(value: T, position: number) {
        //边界判断
        if(position < 0 || position > this.size) return false
        //  先创建节点
        const newNode = new Node<T>(value)
        //  判断是否使头插法
        if (position === 0) {
            newNode.next = this.head
            this.head = newNode
        } else {
            //  双指针
            // let current = this.head
            // let previous: Node<T> | null = null
            // let index = 0
            // while (index++ < position && current) {
            //     previous = current
            //     current = current.next
            // }
            let previous = this.getNode(position - 1)
                newNode.next = previous!.next
                previous!.next = newNode
        }
        this.size++

    }

//    删除节点
    removeAt(position: number): T | null {
    //    边界判断
        if (position < 0 || position >= this.size) return null
        let current = this.head
        if(position === 0) {
            if (this.head === null) return  null
            this.head = current?.next ?? null
        } else {
            //双指针
            // let index = 0
            // let previous: Node<T> | null = null
            // while (index++ < position && current) {
            //     previous = current
            //     current = current.next

            // }
            //单指针
            let previous = this.getNode(position -1)
            previous!.next = previous?.next?.next ?? null
        }
        this.size--
        return current?.value ?? null
    }

//    获取对应位置元素的值
    get(position: number): T | null {
//        边界判断
    if (position < 0 || position >= this.size) return null
    return this.getNode(position)?.value ?? null
    }

//    修改某个节点上的值
    update(value: T, position: number) {
    //      边界判断
        if (position < 0 || position >= this.size) return false
        let current = this.getNode(position)
        current!.value = value
        return true
    }

//    根据值来获取对应位置的索引
    indexOf(value: T): number {
        let current = this.head
        let index = 0
        while (current) {
            if (current.value === value) {
                return index
            }
            index++
            current = current.next
        }
        return -1
    }

//    根据值来删除数据
    remove(value: T): T | null {
        let index = this.indexOf(value)
        return this.removeAt(index)
    }

//    判断链表是否为空
    isEmpty():boolean {
        return  this.size === 0 
    }
}
export {}

设计链表

1
2
3
4
5
6
7
8
9
10
11
```

## 删除链表中的节点

```typescript
//leetcode237
// 他只是值不存在，我可以将下一个节点的值赋值给上一个节点，直接删除下一个节点即可实现
var deleteNode = function(node) {
    node.val = node.next.val
    node.next = node.next.next
};

反转链表

非递归998

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * Definition for singly-linked list.
 * class ListNode {
 *     val: number
 *     next: ListNode | null
 *     constructor(val?: number, next?: ListNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.next = (next===undefined ? null : next)
 *     }
 * }
 */

function reverseList(head: ListNode | null): ListNode | null {
    if(head === null || head.next === null) return head
    let newHead: ListNode | null = null
    while(head) {
        const current = head.next
        head.next = newHead
        newHead = head
        head = current
    }
    return newHead
};

递归999

1
2
3
4
5
6
7
function reverseList(head: ListNode | null): ListNode | null {
    if(head === null || head.next === null) return head
    const newHead = reverseList(head?.next || null)
    head.next.next = head
    head.next = null
    return newHead
};

哈希表

基于数组进行实现

解决冲突

  1. 链地址法

    重复数据采取链表方式进行存储

  2. 开放地址法

    寻找空白单元来添加重复数据

  3. 装填因子 = 总数 / 地址数，越大效率越低；大于0.75扩容

树结构

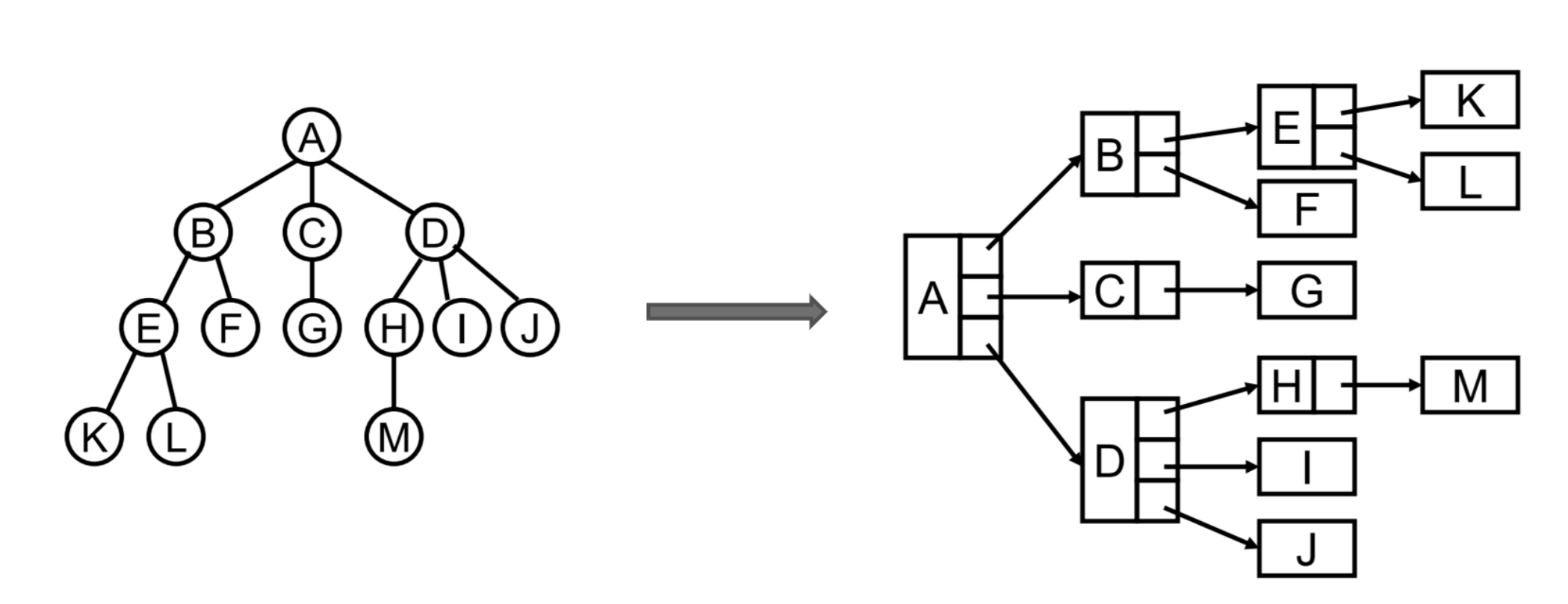
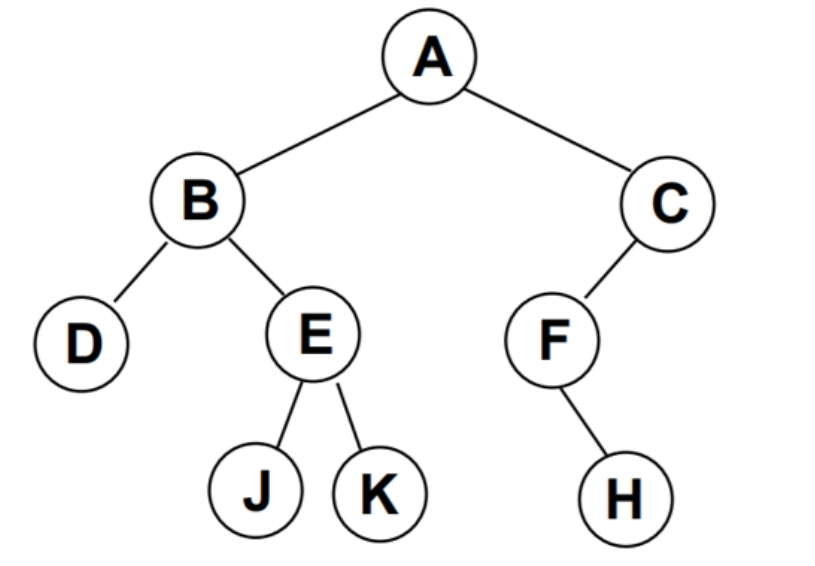
树是由n个节点构成的有限集合

image-20230701164134165

二叉树

  1. 每个树节点都最多只有两个节点
  2. 一棵二叉树第i曾的最大节点数为 2 ^ (n-1)
  3. 深度为k的二叉树有最大节点总数为2^k -1
  4. 二叉树

完美二叉树 | PBT |满二叉树

  1. 在二叉树中，除了最下一层的叶子节点外，每层节点都是2个子节点，就构成满二叉树
  2. 完美二叉树

完全二叉树

  1. 除二叉树最后一层外，其他各层的节点数都达到最大个数
  2. 最后一层从左向右的叶子节点连续存在，只缺右侧若干节点
  3. 完美二叉树是特殊的完全二叉树

二叉搜索树 | 二叉排序树

  1. 非空左子树的所有键值小于根节点的键值
  2. 非空右子树的所有键值大于根节点的键值
  3. 左右子树本身也是二叉搜索树

封装节点

1
2
3
4
5
6
7
8
9
10
class BSTNode<T> {
    value: T
    right: Node<T> | null
    left: Node<T> | null
}

class BSTree<T> {
    
    root: Node<T>
}

常见操作

  1. 插入操作：

    insert(value)：向树中插入一个新的数据。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    insert(value: T) {
            // 1.创建节点
            const newNode = new Node(value)
            // 2. 判断root是否为空
            if(!this.root) {
                this.root = newNode
            }else{ // 节点不为空，找位置进行插入
                this.insertNode(this.root, newNode)
            }
        }
        private insertNode(node:Node<T>, newNode: Node<T>) {
        //    平衡二叉树的特点是左子树值比根小，右子树值比根大
                if(node.value > newNode.value) { //左子树插入数据
                    if(!node.left) {
                        node.left = newNode
                    }else {
                    //    递归调用
                        this.insertNode(node.left, newNode)
                    }
                }else { //右子树插入数据
                    if(!node.right) {
                        node.right = newNode
                    }else {
                        this.insertNode(node.right, newNode)
                    }
                }
            }

  2. 查找操作：

​ search(value)：在树中查找一个数据，如果节点存在，则返回true；如果不存在，则返回false。

​ min：返回树中最小的值/数据。

​ max：返回树中最大的值/数据。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
search(value: T): boolean {
    return this.searchNode(this.root, value)
}
private searchNode(node: Node<T> | null, value: T): boolean {
    if(node === null) return false
//    判断大小
    if(node.value  > value) {
        return  this.searchNode(node.left, value)
    }else if(node.value < value) {
        return  this.searchNode(node.right, value)
    }else {
        return true
    }
}
  1. 遍历操作：

​ inOrderTraverse：通过中序遍历方式遍历所有节点。

​ preOrderTraverse：通过先序遍历方式遍历所有节点。

​ postOrderTraverse：通过后序遍历方式遍历所有节点。

​ levelOrderTraverse：通过层序遍历方式遍历所有节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
  /* 前序遍历 */
  preOrderTraverse(node: Node<T> | null = null) {
      this.preOrderTraverseNode(node)
  }
  private preOrderTraverseNode(node: Node<T> | null = null) {
      if(node) {
          this.preOrderTraverseNode(node.left)
          console.log(node.value)
          this.preOrderTraverseNode(node.right)
      }
  }
  /* 中序遍历 */
  inOrderTraverse(node: Node<T>) {
      this.inOrderTraverseNode(node)
  }
  private inOrderTraverseNode(node: Node<T> | null = null){
      if(node) {
          console.log(node.value)
          this.inOrderTraverseNode(node.left)
          this.inOrderTraverseNode(node.right)
      }
  }
  /* 后序遍历 */
  postOrderTraverse(node: Node<T> | null = null) {
      this.postOrderTraverseNode(node)
  }
  private postOrderTraverseNode(node: Node<T> | null = null) {
  if(node) {
      this.postOrderTraverseNode(node.right)
      this.postOrderTraverseNode(node.left)
      console.log(node.value)
  }
  }
/* 层序遍历 */
  levelOrderTraverse(){
      this.levelOrderTraverseNode()
  }
  private levelOrderTraverseNode() {
      if(!this.root) return
  //    借助队列来完成，建议画图更清晰点
      const queue: Node<T>[] = []
      queue.push(this.root)
      while (queue.length) {
          const current = queue.shift()!
          console.log(current.value)
          if(current.left) {
              queue.push(current.left)
          }
          if(current.right) {
              queue.push(current.right)
          }
      }

  }
  1. 删除操作（有一点点复杂）：

​ remove(value)：从树中移除某个数据。

考虑当前被删除节点是否有子节点，子节点是一个还是两个

优势

  1. 可以快速地找到给定关键字的数据项 并且可以快速地插入和删除数据项。
  2. 如果插入的数据是有顺序的很可能会变成链表，树非常的不平衡不均匀。
  3. 为保证树的查找效率，所以我们在一定程度上需要树保持平衡。

平衡二叉树

图结构（少）

循环链表-shuan

AVL树

堆

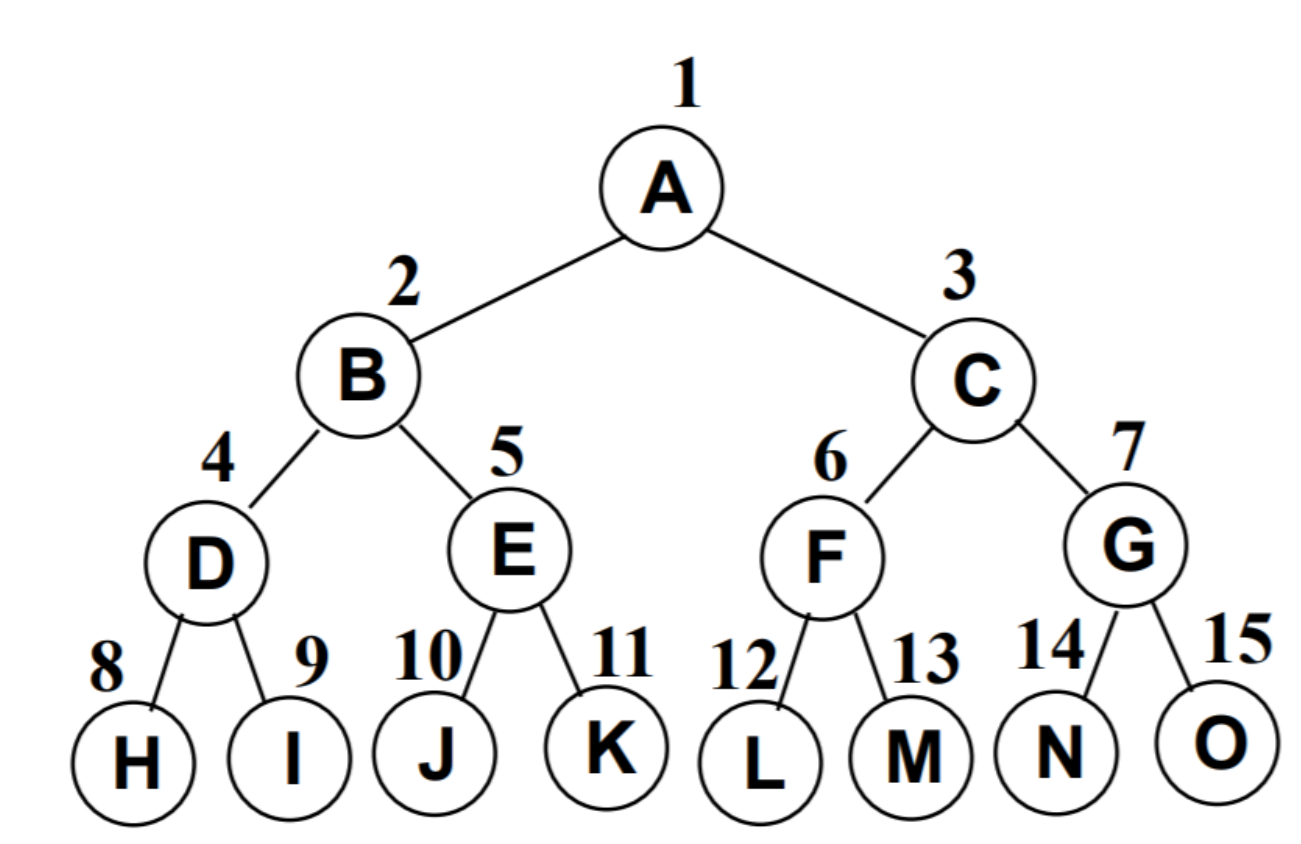
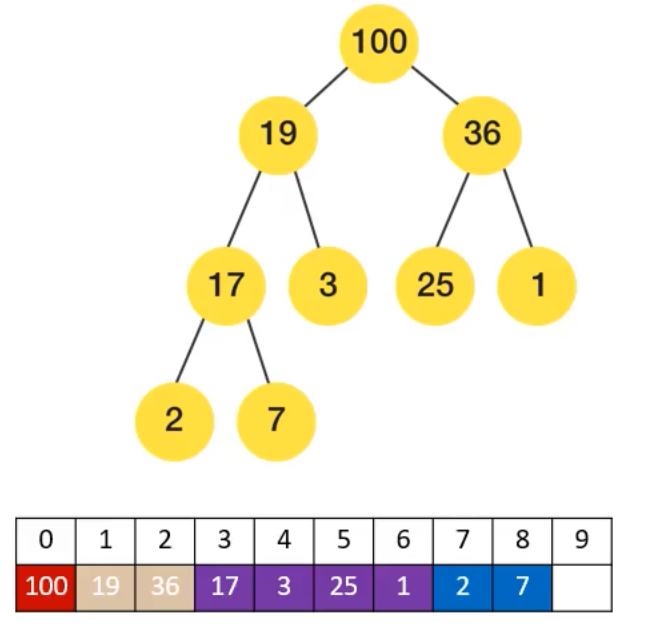
完全二叉树，分最大堆和最小堆

image-20230630101635814

其他

算法复杂度（O）1005

时间复杂度

image-20230626105233684

空间复杂度

二分查找

数组有序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
function binarySearch(array: number[], num: number): number {
    // 定义两个指针
    let left = 0
    let right = array.length - 1
    while (left <=right) {
        let mid = Math.floor((left + right) / 2)
        let minNum = array[mid]
        if(minNum === num) {
            return mid
        }else if(minNum > num) {
            right = mid -1
        }else {
            left = mid + 1
        }
    }

 return -1
}
export {}

定制化输出数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
// 随机生成一个长度为10的整数类型数组，
// 例如 [2， 10， 3， 35， 5， 11， 10， 11， 20]，
// 将其排列成一个新数组，要求新数组形式如下
// [[2, 3, 5], [10, 11], [20], [35]]

// 解题过程
/**
* 1. 随机生成0-99的数据
* 2. 数组去重
* 3. 排序
* 4. 规律存储 0-9 10-19
*/

// 随机生成一个0-1的数，这个数 * max - min + 1 可以获取min的值，再加上min的值就能够获取最大的值
    function getRandomNumber(min1, max1) {
      // 可能存在小数的情况，小的向上取整，大的向下取整
      let min = Math.ceil(min1)
      let max = Math.floor(max1)
      return Math.floor(Math.random() * (max - min + 1) + min)
    };

    // 利用Set数据只能存储一次的特性，进行数组去重
    let initArr = Array.from({ length: 10 }, () => { return getRandomNumber(0, 99) });
    initArr = [... new Set(initArr)];
    initArr.sort((a, b) => a - b);

    const map = {}
    initArr.forEach(item => {
      let key = Math.floor(item / 10)
      if (!map[key]) {
        map[key] = []
      }
      map[key].push(item)
    });

    const result = []
    for (const key in map) {
      result.push(map[key])
    }
    console.log(result)

树状结构转换为平铺属性结构，你会几种写法？

//	方法一：递归
//	每次处理一层结构，通过判断属性的值是否是对象来确定递归是否结束
//	- 如果是对象，则表示递归没有结束，递归调用
//	- 如果不是对象，表示递归的最后一层，确定属性值



//	方法二：while循环-队列
//	使用Object.entries()方法，处理原始对象
//	使用队列存储每一层的值，知道队列中的值处理完毕


# 摩尔投票法
Algorithm
http://example.com/2023/06/15/Algorithm/
作者
Caoqin
发布于
2023年6月15日
许可协议